[K-MOOC | 통계학] 통계학의 이해Ⅰ, 1주차 정리 - 여인권 교수님, 2019년 2학기
안녕하세요. 입문생 Jay입니다. 오늘은 [통계학의 이해Ⅰ] 1 주차 강의를 정리한 후 의문점, 참고사항, 후기를 남기도록 하겠습니다. 참고로 강의 자료를 정리하면서 개인적으로 알고 있는 내용도 덧붙일 예정이라 틀린 내용이 있다면 댓글 주시면 감사하겠습니다.
통계학의 이해 Ⅰ
본 강좌에서는 통계학에서 사용되는 기본 개념과 원리를 이해하고 심화된 통계학을 공부할 수 있는 이론적 기반을 마련할 수 있습니다.
www.kmooc.kr
강의제목, 0주차
- 서론
- 모집단과 표본
- 모집단 종류
- 확률표본추출
- 비확률표본추출
- 정리
- 의문점
- 참고사항
- 후기

서론
이 강의는 1, 2로 나눠져 있습니다. 통계학에 대한 전반적인 지식을 다루고 있습니다. 개론이기 때문에 깊게는 안 들어가지만 통계학에 입문할 때 필요한 지식을 전달하는 것에 의의가 있는 강의입니다. 원래는 1주차씩 보고 정리했는데 이 강의는 고등학교 수학을 공부했다면 별 어려움 없이 공부할 수 있어서 훅훅 넘겼습니다. 그리고 정리하려니 좀 양이 많긴 하네요. 그리고 강의 말미에 R 실습을 통해 통계를 다룰 때 많이 쓰는 무료 프로그램 중 하나인 R에 대한 친숙도도 늘리는 효과를 얻을 수 있습니다.
참고로 전 이 강의가 경쟁 사이트 KOCW의 그 어떤 통계학 강의보다 퀄리티가 낫다고 단언합니다.
1주차 강의에서는 쉬운 개념들을 다룹니다.
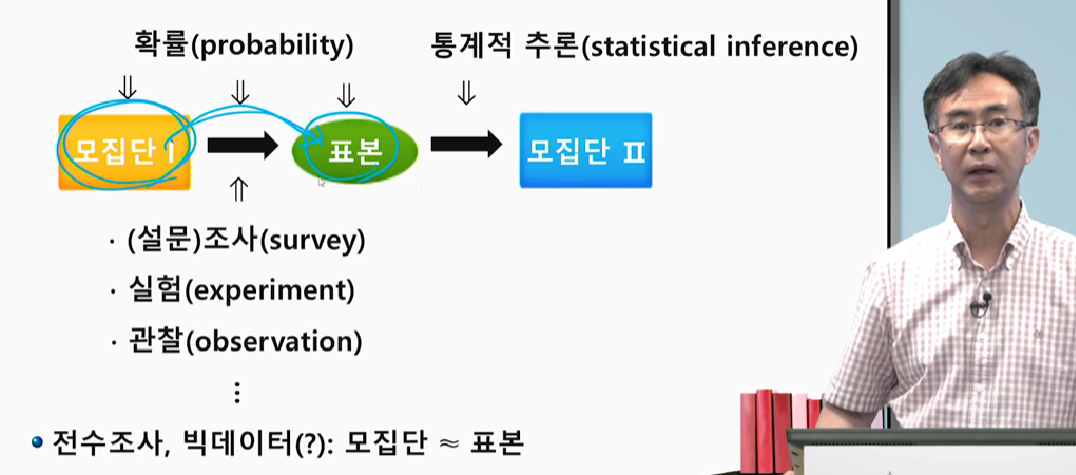
모집단과 표본
모집단(population) : 연구대상이 되는 모든 개체의 집합
전수조사 : 모집단 전체를 대상으로 하는 조사
표본(sample) : 모집단으로부터 선택된 일부의 개체
우리가 실험, 관찰, 전수조사 등을 통해 모집단에서 표본을 뽑을 때, 어떤 표본이 어떤 확률로 뽑힐 지는 알 수 없습니다. 그리고 그 표본을 바탕으로 추론한 모집단이 원래의 모집단과 얼마나 유사한지도 측정하기 어렵습니다.
어떤 모집단에서 얼마만큼 표본을 뽑아야 할지, 그리고 그 표본에서 어떤 추론 과정을 거쳐야 원래의 모집단과 유사한 집합을 얻을지, 이걸 산술적으로 계산하고 해석에 도움을 주는 것이 통계학이죠.

모집단 종류
목표모집단(target population) : 관심대상이 되는 모든 기본단위들의 집합. 시공간상 명확하게 정의된 연구대상 집단.
조사모집단(survey population) : (현실적 제약 고려) 표본추출 대상 기본단위들의 집합
확률표본추출(probability sampling) : 모집단을 구성하는 모든 추출단위에 대해 표본으로 추출된 확률을 알 수 있는 추출법
표본추출틀(표집틀, sampling frame) : 표본으로 추출할 대상이 있는 목록.
통계를 작성하려면 모집단을 조사해야겠죠. 그런데 이 조사방법에도 종류가 있습니다. 크게 목표모집단, 조사모집단이 있습니다. 목표모집단은 우리가 설정한 목표가 되는 대상입니다. 예를 들어 수도권에 거주하는 모든 학부모를 대상으로 조사를 진행을 할 수도 있겠죠. 그런데 이 조사 방식은 수도권에 거주하는 학부모를 전부 기록해놓은 통계가 있어야 하는데, 이런 모집단을 기록해놓은 자료를 표본추출틀이라고 합니다. 여러 이유로 구하기가 까다롭겠죠.
그래서 목표모집단이 아니라, 표본추출틀을 확실하게 구할 수 있는 조사모집단을 고르게 됩니다. 예를 들어서 전화번호부를 통해서 모집단을 확보하는 방식이 있겠죠.

확률표본추출
단순확률추출(simple random sampling) : 크기가 N인 모집단에서 크기 n인 표본을 무작위로 추출
단순확률추출은 거의 사용되지 않지만, 모든 표본추출법의 기초입니다. 표본이 모집단으로부터 뽑힐 확률은 n/N입니다.
계통추출(systemic sampling) : 표집틀에서 k 간격으로 단위들을 표본으로 추출
계통추출은 예를 들어 설명하면, 차량의 출입을 조사하고 싶을 때 첫번째 차량을 시작으로 5번째 차량마다 한 번씩 표본을 뽑는 조사방법을 말합니다. 이때 k=5가 될 테죠. 조사대상은 1+nk (이때 n=1, 2, 3..) 순서의 차가 될 겁니다.
이때 k는 정확도를 고려하여 뽑는데, 보통 모집단이 N개이고 뽑는 표본 개수가 n개라면 k = N/n 을 정해서 뽑습니다. 500개의 차량중에 25개의 차량을 뽑는다면 k = 500/25 = 20이 되겠죠. 그러면 세번째 차량을 시작으로 계통추출한다면 3+nk (이때 k = 20, n = 1, 2, 3...)이 되겠죠. 선거출구조사에서도 자주 활용된다고 합니다.
층화표본추출(cluster random sampling) : 모집단을 서로 중복되지 않은 여러 개의 층(strata)로 나누고, 각 층에서 단순확률추출에 의해 표본을 추출, 부모집단(subpopulation)의 구성내역을 알고 있음.
대한민국은 5천만 국민이 있다고 할 때, 남성과 여성으로 우선 나눌 수 있습니다. 그리고 남성 중에서도 지역별로 나눌 수 있고, 지역 내에서도 소득 순으로 나눌 수 있을 겁니다. 우리가 조사하는 집단은 여러 개의 층으로 갈라져 있다고 할 수 있습니다. 그래서 이 층을 고려하여 표본을 추출하는 걸 층화표본추출이라고 합니다.
성별도 기준이 될 수 있고, 연령도 사람을 특정 층, 집단으로 묶는 기준이 될 수 있습니다. 이때 중요한 건 층마다 성질이 다르다는 점이죠. 다르지 않으면 구분하는 의미가 없을테니까요. 예를 들어 소득 수준을 조사하기 위해 회사원과 고등학생을 나눠서 각기 조사하는 건 의미가 있지만, 시험 성적을 조사하기 위해 고등학생 3학년 중에 생일 별로 집단을 나눈다면 큰 의미가 있을 것 같진 않습니다.
집락추출(stratified sampling) : 서로 인접한 조사단위들을 묶어 구성한 집단(cluster)을 추출하고, 이들 집락 내의 조사단위들을 조사.
모든 집단을 다 조사할 순 없습니다. 표집틀 확보도 어렵고, 대상이 많거나 지역이 너무 넓은 경우 비용이 천문학적으로 들거든요. 조사 대상이 산재돼있기 때문입니다.
이때 모집단 중에서 대표할만한 집단을 선별해서 조사한다면, 비용은 줄면서 신뢰도 높은 통계자료를 얻을 수 있습니다. 예를 들어서 급식 만족도를 위해서 모든 고등학교 학생들을 다 조사할 순 없습니다. 그래서 어느 지역의 어느 고등학교를 뽑고, 고등학교 내에서도 어느 학년이나 학급을 뽑을지를 선정하여 조사할 수 있을 겁니다. 고등학교를 특정한 후 표집틀을 확보하는 건 상대적으로 쉽기 때문입니다. 이때 사용되는게 집락추출입니다.
모든 통계방법은 각기 장점과 단점을 갖고 있기에, 상황에 따라 적절한 방식을 취하는 것이 상당히 중요하겠습니다.

비확률표본추출
비확률표본추출(non-probability sampling) : 특정 표본이 선정된 확률을 알 수 없는 추출법.
[EX] : 편의추출[자발적참여, 설문조사], 유의(purposive)추출[전문가선택], 할당(quota)추출
쉽게 말해서 그냥 임의로 뽑아서 조사하는 걸 말합니다. 랜덤하지도 않고, 표집틀을 확보하기도 쉽지 않습니다. 예를 들어 고등학생 평균 영어 실력을 조사하기 위해 주변 친구들에게 설문조사를 한다든지, 대한민국 평균 소득 수준을 조사하기 위해 강남에 가서 설문지를 돌리는 식입니다. 표본 자체가 편중되거나 오류가 생길 가능성이 높고, 이를 배제할 수 있는 수단도 전무하기에 신뢰도가 낮은 통계가 나오게 됩니다.

가중치
가중치(weight) : 한 표본이 몇 개를 대표하는지 보정해주는 수치
단순확률추출법 가중치 w = N/n
계통추출법 가중치 w = N/n = k
층화추출법 가중치 w : 층의 크기, 표본 크기에 따라 다름
집락추출법 가중치 w : 집락의 크기, 표본 크기에 따라 다름
[EX] : 강의 내에 나온 문제



*[뇌피셜] 어떤 모집단에서 뽑아낸 표본의 가중치를 구하기 위해서는, w = 전체 / 부분 이라는 논리를 적용하면 될 거 같아요. 예를 들어서, 무응답율이 65%일 때, 100명중 65명만 답변했단 뜻이므로 무응답율을 역수를 취하여 100/65를 가중치로 두면 될 것 같습니다. 부분이 얼마만큼 전체를 대표하느냐를 수식적으로 표현한 것이라 이런 논리가 맞아들어가는 듯 해요.

정리
통계학의 의의, 모집단의 정의, 표본의 정의, 표본추출법, 가중치 등을 공부했습니다.
어떤 모집단을 조사하는데 한계가 있기에 표집틀을 확보할 수 있는 자료에 접근하는 것이 효율적이고, 이 표집틀을 어떻게 분석하느냐에 따라 다른 결과가 나올 수 있음을 배웠습니다.
표본이 어느정도로 모집단을 대표하는지 수치로 계산하는 법도 배웠습니다.
그리고 R을 깔아봤네요. 무료 중에는 R이 유명해서 R 프로그래밍을 따로 연구하는 곳도 존재합니다. 다만 실제로 사용해봤을 때는 오류가 생각보다 많이 나는 편입니다. 폰트가 깨지기도 해요.
참고사항
표본추출틀 : https://ko.wikipedia.org/wiki/%ED%91%9C%EC%A7%91%ED%8B%80
후기
통계 기초를 배웠습니다. 고등학교 수학에서는 배울 수 없었던 것을 여기서 배워서 참신한 느낌이었네요. 앞으로도 기대가 됩니다. 물론 한 번 훑었었지만 다시 복습을 하니 까먹었던 걸 다시 리마인드할 수 있어서 좋았습니다.
이만 총총.
※ 이 글은 Windows 11의 whale browser에서 작성됐습니다.
오탈자(誤脫字) 및 비문(非文), 혹은 글이 전하는 정보에 오류가 있는 경우 각 포스트의 댓글로 알려주세요.
최대한 빨리 반영하겠습니다.
감사합니다.